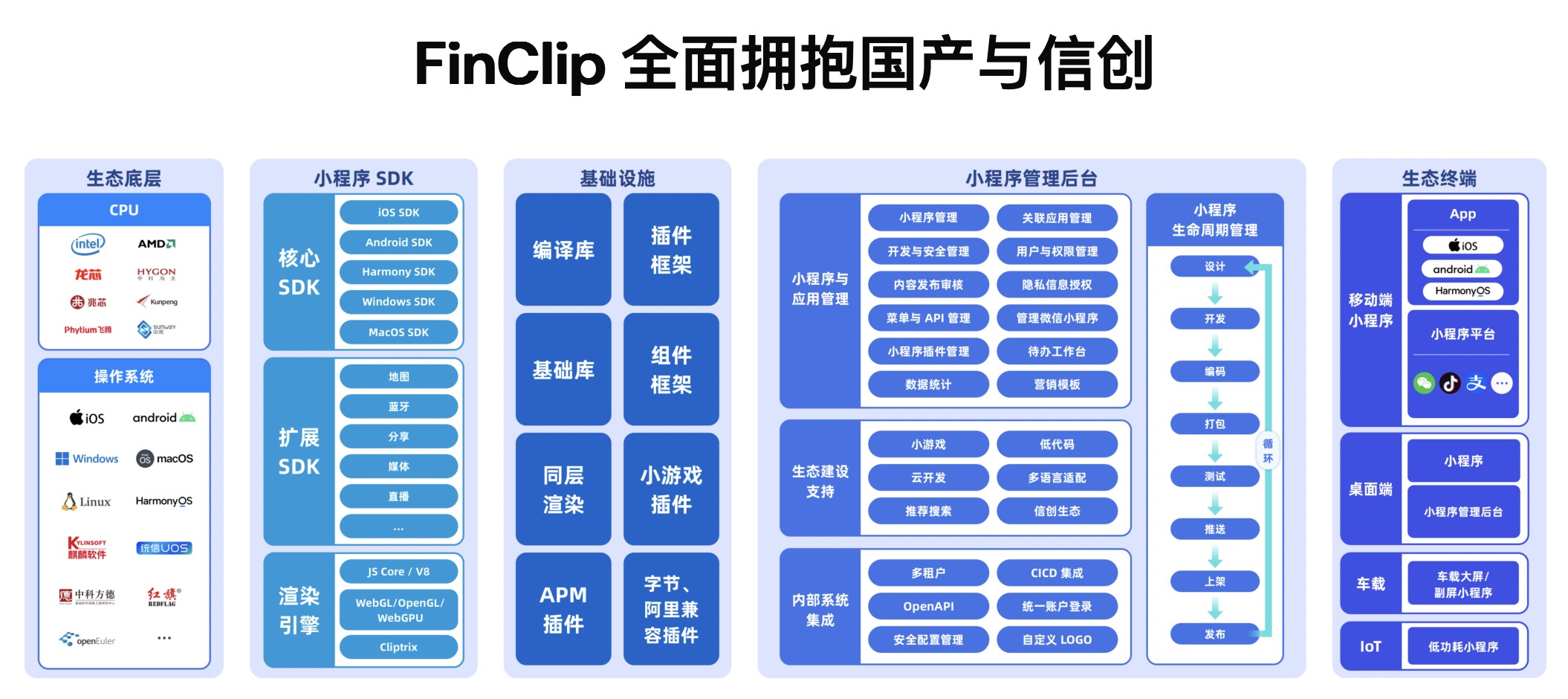
政务服务平台开发需要注意如何提升小程序跨平台兼容性与用户体验
1078
2022-11-13

用Keras解决机器学习问题!
Datawhale干货
作者:皮钱超,厦门大学,Datawhale成员
深度学习框架Keras入门项目
本文介绍3个案例来帮助读者认识和入门深度学习框架Keras。3个案例解决3个问题:回归、二分类、多分类.
本文审稿人:牧小熊,Datawhale成员
Keras官网
为什么选择Keras
相信很多小伙伴在入门深度学习时候首选框架应该是TensorFlow或者Pytorch。在如今无数深度学习框架中,为什么要使用 Keras 而非其他?整理自Keras中文官网:
Keras 优先考虑开发人员的经验Keras 被工业界和学术界广泛采用Keras 可以轻松将模型转化为产品Keras 支持多个后端引擎Keras 拥有强大的多 GPU 和分布式训练支持Keras 的发展得到关键公司的支持,比如:谷歌、微软等
详细信息见中文官网:pandas as pdimport numpy as npimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn import datasets from sklearn.preprocessing import MinMaxScalerfrom sklearn.preprocessing import StandardScalerfrom sklearn.model_selection import train_test_splitimport tensorflow as tffrom keras import modelsfrom keras import layers from keras.models import load_modelnp.random.seed(1234)
回归案例
回归案例中使用的是Keras自带的波士顿房价数据集。
导入数据
In [2]:
from keras.datasets import boston_housing(train_X, train_y), (test_X, test_y) = boston_housing.load_data()
In [3]:
train_X.shape # 数据形状
Out[3]:
(404, 13)
In [4]:
train_X[:3] # 特征向量值
Out[4]:
array([[1.23247e+00, 0.00000e+00, 8.14000e+00, 0.00000e+00, 5.38000e-01, 6.14200e+00, 9.17000e+01, 3.97690e+00, 4.00000e+00, 3.07000e+02, 2.10000e+01, 3.96900e+02, 1.87200e+01], [2.17700e-02, 8.25000e+01, 2.03000e+00, 0.00000e+00, 4.15000e-01, 7.61000e+00, 1.57000e+01, 6.27000e+00, 2.00000e+00, 3.48000e+02, 1.47000e+01, 3.95380e+02, 3.11000e+00], [4.89822e+00, 0.00000e+00, 1.81000e+01, 0.00000e+00, 6.31000e-01, 4.97000e+00, 1.00000e+02, 1.33250e+00, 2.40000e+01, 6.66000e+02, 2.02000e+01, 3.75520e+02, 3.26000e+00]])
In [5]:
train_y[:3] # 标签值
Out[5]:
array([15.2, 42.3, 50. ])
数据标准化
神经网络中一般输入的都是较小数值的数据,数据之间的差异不能过大。现将特征变量的数据进行标准化处理
In [6]:
train_X[:3] # 处理前
Out[6]:
array([[1.23247e+00, 0.00000e+00, 8.14000e+00, 0.00000e+00, 5.38000e-01, 6.14200e+00, 9.17000e+01, 3.97690e+00, 4.00000e+00, 3.07000e+02, 2.10000e+01, 3.96900e+02, 1.87200e+01], [2.17700e-02, 8.25000e+01, 2.03000e+00, 0.00000e+00, 4.15000e-01, 7.61000e+00, 1.57000e+01, 6.27000e+00, 2.00000e+00, 3.48000e+02, 1.47000e+01, 3.95380e+02, 3.11000e+00], [4.89822e+00, 0.00000e+00, 1.81000e+01, 0.00000e+00, 6.31000e-01, 4.97000e+00, 1.00000e+02, 1.33250e+00, 2.40000e+01, 6.66000e+02, 2.02000e+01, 3.75520e+02, 3.26000e+00]])
针对训练集的数据做标准化处理:减掉均值再除以标准差
In [7]:
mean = train_X.mean(axis=0) # 均值train_X = train_X - mean # 数值 - 均值std = train_X.std(axis=0) # 标准差train_X /= std # 再除以标准差train_X # 处理后
针对测集的数据处理:使用训练集的均值和标准差
In [8]:
test_X -= mean # 减掉均值test_X /= std # 除以标准差
构建网络
In [9]:
train_X.shape
Out[9]:
(404, 13)
In [10]:
model = models.Sequential()model.add(tf.keras.layers.Dense(64, activation="relu", input_shape=(train_X.shape[1], )))model.add(tf.keras.layers.Dense(64, activation="relu"))model.add(tf.keras.layers.Dense(1)) # 最后的密集连接层,不用激活函数model.compile(optimizer="rmsprop", # 优化器 loss="mse", # 损失函数 metrics=["mae"] # 评估指标:平均绝对误差 )
网络架构
In [11]:
model.summary()
训练网络
In [12]:
history = model.fit(train_X, # 特征 train_y, # 输出 epochs = 100, # 模型训练100轮 validation_split=0.2, batch_size=1, verbose=0 # 静默模式;如果=1表示日志模式,输出每轮训练的结果 )
保存模型
In [13]:
model.save("my_model.h5") # 保存模型del model # 删除现有的模型
In [14]:
model = load_model('my_model.h5') # 加载模型
评估模型
返回的是loss和mae的取值
In [15]:
model.evaluate(test_X, test_y)4/4 [==============================] - 0s 6ms/step - loss: 16.1072 - mae: 2.5912
Out[15]:
[16.107179641723633, 2.5912036895751953]
history对象
In [16]:
type(history) # 回调的History对象
Out[16]:
keras.callbacks.History
In [17]:
type(history.history) # 字典
Out[17]:
dict
In [18]:
查看history.history字典对象中的信息:keys就是每个评价指标,values其实就是每次输出的指标对应的值
for keys,_ in history.history.items(): print(keys)lossmaeval_lossval_mae
In [19]:
len(history.history["loss"])
Out[19]:
100
In [20]:
history.history["loss"][:10]
Out[20]:
[197.65003967285156, 32.76368713378906, 22.73907470703125, 18.689529418945312, 16.765336990356445, 15.523008346557617, 14.131484985351562, 13.04631519317627, 12.62230396270752, 12.256169319152832]
loss-mae
In [21]:
# 损失绘图import matplotlib.pyplot as plthistory_dict = history.history loss_values = history_dict["loss"]mae_values = history_dict["mae"]epochs = range(1,len(loss_values) + 1)# 训练plt.plot(epochs, # 循环轮数 loss_values, # loss取值 "r", # 红色 label="loss" )plt.plot(epochs, mae_values, "b", label="mae" )plt.title("Loss and Mae of Training")plt.xlabel("Epochs")plt.legend()plt.show()
二分类
使用的是sklearn中自带的cancer数据集
导入数据
In [22]:
cancer=datasets.load_breast_cancer()cancer
部分数据信息截图
# 生成特征数据和标签数据X = cancer.datay = cancer.target
数据标准化
In [24]:
X[:2] # 转换前
Out[24]:
array([[1.799e+01, 1.038e+01, 1.228e+02, 1.001e+03, 1.184e-01, 2.776e-01, 3.001e-01, 1.471e-01, 2.419e-01, 7.871e-02, 1.095e+00, 9.053e-01, 8.589e+00, 1.534e+02, 6.399e-03, 4.904e-02, 5.373e-02, 1.587e-02, 3.003e-02, 6.193e-03, 2.538e+01, 1.733e+01, 1.846e+02, 2.019e+03, 1.622e-01, 6.656e-01, 7.119e-01, 2.654e-01, 4.601e-01, 1.189e-01], [2.057e+01, 1.777e+01, 1.329e+02, 1.326e+03, 8.474e-02, 7.864e-02, 8.690e-02, 7.017e-02, 1.812e-01, 5.667e-02, 5.435e-01, 7.339e-01, 3.398e+00, 7.408e+01, 5.225e-03, 1.308e-02, 1.860e-02, 1.340e-02, 1.389e-02, 3.532e-03, 2.499e+01, 2.341e+01, 1.588e+02, 1.956e+03, 1.238e-01, 1.866e-01, 2.416e-01, 1.860e-01, 2.750e-01, 8.902e-02]])
In [25]:
ss = StandardScaler()X = ss.fit_transform(X)X[:2] # 转换后
Out[25]:
array([[ 1.09706398e+00, -2.07333501e+00, 1.26993369e+00, 9.84374905e-01, 1.56846633e+00, 3.28351467e+00, 2.65287398e+00, 2.53247522e+00, 2.21751501e+00, 2.25574689e+00, 2.48973393e+00, -5.65265059e-01, 2.83303087e+00, 2.48757756e+00, -2.14001647e-01, 1.31686157e+00, 7.24026158e-01, 6.60819941e-01, 1.14875667e+00, 9.07083081e-01, 1.88668963e+00, -1.35929347e+00, 2.30360062e+00, 2.00123749e+00, 1.30768627e+00, 2.61666502e+00, 2.10952635e+00, 2.29607613e+00, 2.75062224e+00, 1.93701461e+00], [ 1.82982061e+00, -3.53632408e-01, 1.68595471e+00, 1.90870825e+00, -8.26962447e-01, -4.87071673e-01, -2.38458552e-02, 5.48144156e-01, 1.39236330e-03, -8.68652457e-01, 4.99254601e-01, -8.76243603e-01, 2.63326966e-01, 7.42401948e-01, -6.05350847e-01, -6.92926270e-01, -4.40780058e-01, 2.60162067e-01, -8.05450380e-01, -9.94437403e-02, 1.80592744e+00, -3.69203222e-01, 1.53512599e+00, 1.89048899e+00, -3.75611957e-01, -4.30444219e-01, -1.46748968e-01, 1.08708430e+00, -2.43889668e-01, 2.81189987e-01]])
数据集划分
In [26]:
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=123)X_train.shape
Out[26]:
(455, 30)
In [27]:
y_train.shape
Out[27]:
(455,)
In [28]:
X_test.shape # 测试集长度是114
Out[28]:
(114, 30)
构建网络
这是一个二分类的问题,最后一层使用sigmoid作为激活函数
In [29]:
model = models.Sequential()# 输入层model.add(tf.keras.layers.Dense(16, activation="relu", input_shape=(X_train.shape[1],)))# 隐藏层model.add(tf.keras.layers.Dense(16, activation="relu"))# 输出层model.add(tf.keras.layers.Dense(1, activation="sigmoid"))
网络架构
In [30]:
model.summary()
编译模型
在keras搭建的神经网络中,如果输出是概率值的模型,损失函数最好使用:交叉熵crossentropy
常用目标损失函数的选择:
binary_crossentropy:针对二分类问题的交叉熵categorical_crossentropy:针对多分类问题的交叉熵
两种不同的指定方法:
# 方法1model.compile(loss='mean_squared_error', optimizer='rmsprop')# 方法2from keras import lossesmodel.compile(loss=losses.mean_squared_error, optimizer='rmsprop')
常用的性能评估函数:
binary_accuracy: 针对二分类问题,计算在所有预测值上的平均正确率categorical_accuracy:针对多分类问题,计算再所有预测值上的平均正确率sparse_categorical_accuracy:与categorical_accuracy相同,在对稀疏的目标值预测时有用
In [31]:
# 配置优化器from keras import optimizersmodel.compile(optimizer="rmsprop", # 优化器 loss="binary_crossentropy", # 目标损失函数 metrics=["acc"] # 评价指标函数 acc--->accuracy )
训练网络
In [32]:
len(X_train)
Out[32]:
455
In [33]:
history = model.fit(X_train, # 特征向量 y_train, # 标签向量 epochs=20, # 训练轮数 batch_size=25 # 每次训练的样本数 )history
评估模型
In [34]:
model.evaluate(X_test, y_test)4/4 [==============================] - 0s 3ms/step - loss: 0.0879 - acc: 0.9825
Out[34]:
[0.08793728798627853, 0.9824561476707458]
可以看到模型的精度达到了惊人的98.2%!
loss-acc
In [35]:
for keys, _ in history.history.items(): print(keys)lossacc
In [36]:
# 损失绘图import matplotlib.pyplot as plthistory_dict = history.history loss_values = history_dict["loss"]acc_values = history_dict["acc"]epochs = range(1,len(loss_values) + 1)# 训练plt.plot(epochs, # 循环轮数 loss_values, # loss取值 "r", # 红色 label="loss" )plt.plot(epochs, acc_values, "b", label="acc" )plt.title("Loss and Acc of Training")plt.xlabel("Epochs")plt.legend()plt.show()
可以看到:随着轮数的增加loss在逐渐降低,而精度acc在逐渐增加,趋近于1
多分类案例
多分类的案例使用sklearn中自带的iris数据集,数据集不多介绍。最终结果是存在3个类的。
导入数据
In [37]:
iris = datasets.load_iris()
In [38]:
# 特征数据和标签数据X = iris.datay = iris.targetX[:2]
Out[38]:
array([[5.1, 3.5, 1.4, 0.2], [4.9, 3. , 1.4, 0.2]])
In [39]:
y[:3]
Out[39]:
array([0, 0, 0])
数据标准化
In [40]:
ss = StandardScaler()X = ss.fit_transform(X)
数据集划分
In [41]:
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=123)X_train.shape
Out[41]:
(120, 4)
标签向量化
In [42]:
y_test[:5] # 转换前
Out[42]:
array([1, 2, 2, 1, 0])
In [43]:
# 内置方法实现标签向量化from keras.utils.np_utils import to_categoricaly_train = to_categorical(y_train)y_test = to_categorical(y_test)
In [44]:
y_test[:5] # 转换后
Out[44]:
array([[0., 1., 0.], [0., 0., 1.], [0., 0., 1.], [0., 1., 0.], [1., 0., 0.]], dtype=float32)
In [45]:
X_train[:3]
Out[45]:
array([[ 1.88617985, -0.59237301, 1.33113254, 0.92230284], [ 0.18982966, -1.97355361, 0.70592084, 0.3957741 ], [-1.38535265, 0.32841405, -1.22655167, -1.3154443 ]])
构建模型
In [46]:
model = models.Sequential()model.add(tf.keras.layers.Dense(64, activation="relu", input_shape=(X_train.shape[1],)))model.add(tf.keras.layers.Dense(64, activation="relu"))model.add(tf.keras.layers.Dense(3, activation="softmax"))
模型编译
多分类问题一般是使用categorical_crossentropy作为损失函数。它是用来衡量网络输出的概率分布和标签的真实概率分布的距离。
In [47]:
model.compile(optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"] )
训练网络
In [48]:
len(X_train)
Out[48]:
120
In [49]:
history = model.fit(X_train, y_train, epochs=10, batch_size=15 )history
评估模型
In [50]:
model.evaluate(X_test, y_test)1/1 [==============================] - 0s 414ms/step - loss: 0.1799 - accuracy: 1.0000
Out[50]:
[0.17986173927783966, 1.0]
loss-acc曲线
In [51]:
for keys, _ in history.history.items(): print(keys)lossaccuracy
In [52]:
# 损失绘图import matplotlib.pyplot as plthistory_dict = history.history loss_values = history_dict["loss"]acc_values = history_dict["accuracy"]epochs = range(1,len(loss_values) + 1)# 训练plt.plot(epochs, # 循环轮数 loss_values, # loss取值 "r", # 红色 label="loss" )plt.plot(epochs, acc_values, "b", label="accuracy" )plt.title("Loss and Accuracy of Training")plt.xlabel("Epochs")plt.legend()plt.show()
上面的方案只是从最基本的流程来学习如何使用Keras框架来进行神经网络的建模,还有很多可以深入学习和挖掘的点:
1. 验证集数据的引入
2. 加入正则化技术,防止模型过拟合
3. 如何评估训练的轮次,使得模型在合适时机停止
4. 激活函数的选择等
整理不易,点赞三连↓
版权声明:本文内容由网络用户投稿,版权归原作者所有,本站不拥有其著作权,亦不承担相应法律责任。如果您发现本站中有涉嫌抄袭或描述失实的内容,请联系我们jiasou666@gmail.com 处理,核实后本网站将在24小时内删除侵权内容。
发表评论
暂时没有评论,来抢沙发吧~